ai产品经理必会知识点! 一文读懂, LLM大语言模型的工作原理。

大家好，我是喜欢研究AI的一枚产品经理

平时主要从事与AI、大模型、智能座舱等相关工作。在这里，我会持续跟大家分享AI相关的前沿技术、产品体验、个人心得等有营养有价值的信息

另外，我还超爱自驾游~

导语：

从前年爆火的GPT，到今年过年期间惊叹世人的DeepSeek，如今，AI、人工智能、大模型这些词汇对于大家来说不但不陌生，反而从各种各样的AI应用和产品中，我们已经有了切身的体会。

但是，除了用过和会用，有多少人真正了解LLM的本质究竟是什么？它的工作原理究竟是怎么运行的？

可能这个问题对于普通人来说，duck不必知其所以然，但对于想要从事ai行业，尤其是ai产品经理和ai工程师的伙伴们，这个可是必备知识点！

这篇文章，我想从非纯底层技术的角度，而是从整体框架层，从产品经理的视角，通过举例和图示，尽量言简意赅的阐述LLM的本质。因此我将通过10张图和三部分内容，统计与概率、大模型推理预测机制、temperature（温度参数）入手，让不懂技术的你，也能了解LLM的工作原理。

好了，接下来，我们就看图说话。

一、统计与概率

LLM的本质是基于统计模式学习语言的模型，所以理解什么是数据总体（海量的文本语料库）、如何计算基本事件（如某个词出现）的概率，是理解LLM工作原理的第一步。它建立了“概率描述偏好/可能性”的直观感受。

所以，开篇我会用网球和足球来举例子，先让大家理解概率分布和统计的思维。

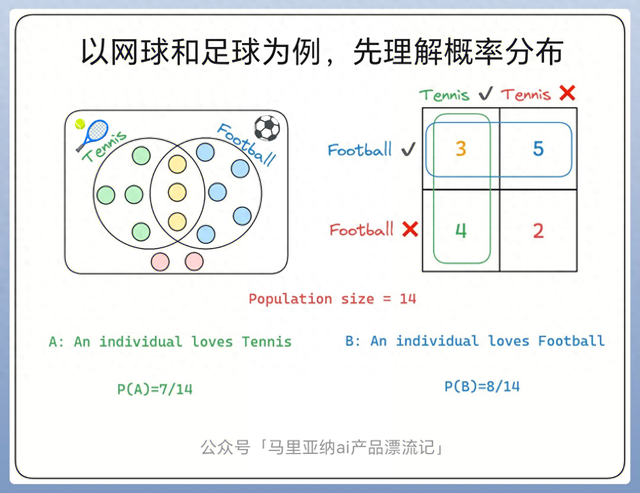
上图是一个共14人的运动队，图中的Population可以理解为总体、总人数，即总人数是14人。

然后，其中有人喜欢网球、有人喜欢足球，有人同时喜欢两者，但是也有人两个都不喜欢。对应到图中，喜欢网球的人是绿色圈圈，共4人；喜欢足球⚽️的人是蓝色圈圈，共5人；既喜欢网球又喜欢足球的是黄色圈圈，共3人；两者都不喜欢的是粉色圈圈，共2人；一共是4+5+3+2=14人。

继续看图，右上方2x2的表格，用来直观的进行数学统计，即：

网球 & 足球：3人 (即A∩B)

网球 & ❌足球：4人

❌网球 & 足球：5人

❌网球 & ❌足球：2人

那么基于表格所示，可以统计基本概率：

P(A)：喜欢网球的概率 = 喜欢网球的人数(7) / 总人数(14) = 7/14

P(B)：喜欢足球的概率 = 喜欢足球的人数(8) / 总人数(14) = 8/14

上面这张条件概率图，是建立在第一张基本概率图的基础上来的，这里我们引入一个新的，但是非常关键的概念——条件概率 P(A|B)，这直接关系到LLM如何根据上下文预测下一个词！

延续图1，这张图2我们先了解一个概念：联合概率 P(A∩B)，意思就是既喜欢网球也喜欢足球的概率 = 同时喜欢两者的人数(3) / 总人数(14) = 3/14。

那紧接着就是条件概率 P(A|B)，就是在已知某人喜欢足球（事件B发生）的条件下，ta也喜欢网球（事件A发生）的概率。

条件概率计算公式： P(A|B) = P(A∩B) / P(B)，代入数值： P(A|B) = (3/14) / (8/14) = 3/8，意思是如果你在人群中随机拉出来一个喜欢足球的人（8人），这其中有3人同时也喜欢网球。所以，在这个“喜欢足球”的小圈子里，喜欢网球的比例是3/8。这就是条件概率的意义——它限定了样本空间（只在喜欢足球的人里面考虑）。

那么回到LLM，LLM预测下一个词的核心机制就是计算条件概率！理解了这个概念后，马上看下图图3，给定前面的词语序列（“The boy went to the”），计算下一个词是“Playground”、“Park”、“School”等的概率 P(下一个词 | 前面的上下文)。这里LLM对于下一个词的预测，就跟图2展示的 P(A|B) 计算原理一模一样，即事件B是“前面的上下文”，事件A是“可能的下一个候选词”。

二、LLM推理预测机制

图3，这张图非常形象地说明了LLM在做什么。它接收了一段文字（上下文“the boy went to the”），然后就像一个极其熟悉语言规律的“概率预测机”，尝试推测接下来最应该出现什么词。（后面出来的这些词，是通过向量计算得出来的，这个概念，大家也可以翻看我之前的另一篇文章），这就是图2条件概率在实际语言任务中的直接应用。

具体来拆解分析下图3，从左到右看。

首先，图中绿色字体写明了“Previous words (Context)”——即已有的、输入给LLM的文本序列：“The boy went to the”。

然后，LLM的任务就是基于这个“上下文”，预测接下来最有可能出现的单词是什么。图中展示了几个可能的下一个词作为例子：“Cafe”、“Hospital”、“Playground”、“Park”、“School”。

注意： LLM不会只给出一个“最可能”的答案（如“School”），它会为所有可能的单词（这里方便举例只写了几个，实际可能是成千上万个！）计算一个概率 P(单词 | 'The boy went to the')。

这张图图4，就具体化展示了LLM的预测过程，它如何为每个可能的词输出一个概率值，并形成概率分布，以及初始的选择策略——选概率最高的。

我们分步来看图4的过程：

输入： 就是图3的上下文“The boy went to the”。

模型： 大脑图标代表模型本身。

输出： 概率分布，这是核心！LLM为词汇表（所有它学过的词）里的每个词计算出一个概率值，数值在0到1之间，并且所有词的概率总和为1。

可视化： 图中展示了5个代表性候选词及其计算出的示例概率：Playground(0.4), School(0.3), Park(0.15), Cafe(0.1), Hospital(0.05)。

初始策略（Greedy Search）： 图片右下角底部用紫色小字备注了“word with highest probability is chosen（选择概率最高的单词）”。这种情况下，会输出“Playground”（概率0.4是最高的）。这是一种最直接、最确定性的选择方式。

图1 - 图4，其实已经把LLM的工作过程展示完了，但是，那只是最理想化、最简化的描述。所以图5，要继续给大家说明LLM是如何自我“学习”并改进预测能力的——通过计算预测错误并进行反向传播调整，可以理解为“强化学习、奖励机制”这类概念。

图片标题“Loss calculation”是损失计算的意思，它的作用就是让模型有自我学习、修正和优化的内部机制，那对于用户来说，就是越用这个模型，感觉它越聪明。

所以，这张图就是跟大家解释，不是说LLM预测出来下一个词是什么，就直接输出了，它还会通过其他的计算，进行进一步的判断，然后才会输出最终结果。并且，在这个“预测->计算损失->微调内部参数->再预测”的过程中，大模型也完成了“自我提升”。

因此，这张图里涉及到对数、交叉熵这些数学计算，可能很多人不懂，但你只要理解上面的解释也ok的。

还是分步解释下上图里面各种公式计算的过程：

输入： 仍然是上下文“The boy went to the”。

预测： “LLM”模型输出了每个词的概率分布（与图4一样）。

真实值 (Ground Truth)： 在训练阶段，我们知道这个上下文之后实际上出现的词是什么。图中假设正确答案是“Playground”，所以“Playground”位置是1，其余词位置都是0 (图中列出只有这几个词，实际词汇表所有位置都要看)。

计算损失(Loss)： 我们需要衡量模型的预测值(P(Playground)=0.4)与真实值(Playground=1)之间的差距。

损失函数公式： Loss = -log(P(正确答案对应的概率))

代入： Loss = -log(P('Playground' | 'The boy went to the')) = -log(0.4) ≈ -(-0.916) ≈ 0.916（log是自然对数，log(0.4) ≈ -0.916）。

损失的意义： 预测概率越高（越接近1），损失值越低（越接近0）。预测概率越低（越接近0），损失值急剧升高。模型在训练中会不断尝试最小化整个训练数据的平均损失。通过计算损失并应用反向传播算法调整LLM内部的参数（神经网络的权重），模型就能逐渐提高预测的准确性。

三、Temperature温度调控LLM的预测随机性

好了，上面5张图基本概述完了LLM的工作流程。从图6开始，再引入一个关键词“Temperature温度”，它是影响LLM的一个关键参数！换句话说，同样一个大模型，给它输入同一个问题，但是Temperature的不同，会导致LLM的输出结果天壤之别。

可能有很多实践过大模型的朋友会了解，就是我们通过扣子或dify这类平台，去调试大模型的时候，一般页面上都会有一个Temperature的可自定义参数，这个参数你设置的越小，它输出的结果就越“中规中矩和刻板”，你设置的参数值越大，它输出的结果就越“有创意或天马行空”，这就是Temperature的作用。

上图6和下图7，就是一个对比，通过code的形式，跟大家展示低温和高温，对于LLM输出结果的影响。

上图6，temperature=0.1**50（这个值极其接近0）

给模型相同的输入（提示语“Continue this: In 2013, ...”）

输出： 连续运行了两次，两次输出的文本完全一模一样——“The world was captivated by the birth of Prince George...”。

结果说明： 图中黑色粗体字标注“Temperature close to zero”和“Identical response”。低温会极大程度地尖锐化输出概率分布（放大最高概率项，抑制其他项）。当温度趋近0时，模型实际上变成了只选择可能性最大的下一个词（类似图4的Greedy Search策略）。这使得生成文本高度确定、一致且相对保守（重复输入可能稍有波动，但极低温下波动极小）。

看完图6，继续看图7↑ 显然，图7中T的值大于1，那么它的输出将会是高度随机的，完全无规律。

上图7，与图6相似的代码，但设置了一个很高的温度 temperature=2

同样的输入（“Continue this: In 2013, ...”）

输出： 图中打印出的内容是一长串完全混乱、没有语义连贯性的字符、无意义词和符号组合（...infection,-your PSD surgicalPYTHON**...）

结果说明： 图中黑色粗体字标注“Random output”，就是说高温会平滑化输出概率分布，让原本低概率的词获得相对更高的机会被选中。当温度非常高时，所有词的概率几乎变得均匀，模型变成了完全随机的字符生成器，丢失了所有上下文相关性和语义信息。输出的就是近乎噪声的乱码。

这张图，重点在于sampling，采样！就是说，LLM在生成文本时（推理阶段），是如何利用概率分布进行采样(Sampling) 来获得随机但有控制的输出，而非总是选择最高概率词。

这张图，进一步概述了LLM非常重要的一个工作机制：基于模型的概率分布进行采样。与图4只选最高概率词（Greedy）和图6低温（接近Greedy）不同，采样是文本生成（如聊天、创作）中自然引入随机性和创造性的方式。

上图8，从左到右，我们依次来看：

最左侧输出层(Output layer): 模型输出的原始分数，每个可能的下一个词（Token）对应一个分数（Logits）。Logits: 这些分数本身数值范围没有限制。Softmax层: 将Logits转换成合法的概率分布（所有值在0-1之间，总和为1），每个Token对应的Softmax转换后的概率值（Token 1:0.86, Token 2:0.00等）。

图片右侧黄色小字“Sample from this distribution”，是说从该分布中采样。

采样： 不是简单地挑选概率最高的Token（Token 1:86%），而是根据每个Token的概率值大小，随机地选择下一个Token。例如，一个概率为50%的词，被选中的可能性就是50%；一个概率为1%的词，被选中的可能性就是1%。这使得输出具有多样性。

图9，是用数学公式展示了温度T是如何改变Softmax计算结果的。这张图重在展示图6、7、8背后的底层数学原理。温度，通过一个数学变换（缩放Logits），控制了Softmax输出的概率分布的集中度(Sharpness)/均匀度(Uniformity)。

这张图，以及最后一张图10，不理解没关系，也可以不看，只是为了补充背后的数学原理。

核心：Logits，模型输出的原始分数。

传统Softmax： 公式 σ(z)_i = e^{z_i} / Σ_j e^{z_j}e^{z_i}: 某个词i原始分数的指数。Σ_j e^{z_j}: 所有词原始分数指数的总和。结果：原始分数大的词获得较高概率。

温度调整Softmax： 公式 σ(z, T)_i = e^{(z_i / T)} / Σ_j e^{(z_j / T)}变化点: 每个原始分数 z_i 在计算前都除以温度 T (z_i / T)。

温度T的作用：T小 (接近0)： z_i / T 值会被放大。最大值被放大的程度远大于其他值，导致e^{(最大值/T)}变得极大。最终概率分布变得尖锐（一个词概率接近1，其余接近0）。这就是图6（低温）确定性的数学来源。T大 (>>1)： z_i / T 值被缩小。所有原始分数的差距被压缩。最终概率分布变得平滑、均匀。这就是图7（高温）乱码和图8中低概率词有机会被采样的数学来源。

最后这张图，就用具体的数值计算例子，直观地验证图9理论，同时也形象再现了图6和图7的效果。通过它可看到温度这个单一参数如何通过在Softmax公式里缩放原始分数，来控制模型输出的“冒险/保守”程度。

输入数组a = [1, 2, 3, 4]，这可以看作4个词的Logits（原始分数）。

计算1：原始Softmax(a)，结果是[0.03, 0.09, 0.24, 0.64]。最大值4对应的概率0.64显著高于其他值，分布较尖锐。

计算2：低温 (T=0.01)下的Softmax(a/T)：a/T = [1/0.01=100, 2/0.01=200, 3/0.01=300, 4/0.01=400]。Softmax结果：[5.12e-131, 1.38e-087, 3.72e-044, **1.00e+000**] ≈ [0, 0, 0, 1]。结果：概率分布极其尖锐！原始最高值4对应概率几乎是1，其他词概率几乎为0。 对应图6的确定性输出。

计算3：高温 (T=1e9)下的Softmax(a/T)：a/T = [1e-9, 2e-9, 3e-9, 4e-9]。所有值都变得非常小且彼此接近。Softmax结果：[0.25, 0.25, 0.25, 0.25]。结果：概率分布几乎完全均匀！ 每个词的概率都是25%，失去了Logits提供的偏好信息。对应图7的乱码和高度随机性。

好了，以上就是本文的全部内容了，如果喜欢或者觉得对你有点用处，欢迎点赞分享

✏️体验分享AI前沿技术与产品｜记录分享个人学习与心得｜情绪价值传播｜链接同行者！